 Complex numbers refer to an entity of the form (a+i b), where ‘a’ and ‘b’ are real numbers, i = Ö-1 and ib is called imaginary part.
Complex numbers refer to an entity of the form (a+i b), where ‘a’ and ‘b’ are real numbers, i = Ö-1 and ib is called imaginary part.
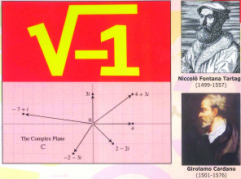
Before 16th century, concept of square root of negative number was non-existent. This created problem as mathematicians were not able to solve polynomial equations. Finally concept of complex number was formulated that extended the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part.
Complex numbers are used in many scientific fields, including engineering, electromagnetism, quantum physics, applied mathematics, and chaos theory.
The equation X2+1=0 has no real solution, since the square of a real number is 0 or positive. Complex numbers provide a solution to this problem. The idea is to enhance the real numbers by introducing a non-real number i whose square is -1, so that the solutions to the preceding equation are x = i and x = -i.
Italian mathematician Gerolamo Cardano, while working on a problem of general polynomial, conceived the idea of complex numbers in around 1545. This ultimately led to the fundamental theorem of algebra : every non-constant single-variable polynomial with complex coefficients has at least one complex root. Thus complex number form an algebraically close field, where any polynomial equation has a root.
Many mathematicians contributed to the full development of complex numbers. The rules for addition, subtraction, multiplication, and division of complex numbers were developed by the Italian mathematician Rafael Bombelli. A more abstract formalism for the complex numbers was further developed by the Irish mathematician William Rowan Hamilton.














Comments